ব্যাংক জব নিয়োগ পরীক্ষা – গণিত – Areas & Volumes

1. CUBOID

   Let length = l, breadth = b and height = h units. Then

   1. Volume = (l x b x h) cubic units.
   2. Surface area = 2(lb + bh + lh) sq. units.
   3. Diagonal = l² + b² + h² units.
2. CUBE

   Let each edge of a cube be of length a. Then,

   1. Volume = a³ cubic units.
   2. Surface area = 6a² sq. units.
   3. Diagonal = 3a units.
3. CYLINDER

   Let radius of base = r and Height (or length) = h. Then,

   1. Volume = (r²h) cubic units.
   2. Curved surface area = (2rh) sq. units.
   3. Total surface area = 2r(h + r) sq. units.
4. CONE

   Let radius of base = r and Height = h. Then,

   1. Slant height, l = h² + r² units.
   2. Volume = r²h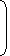 cubic units.
   3. Curved surface area = (rl) sq. units.
   4. Total surface area = (rl + r²) sq. units.
5. SPHERE

   Let the radius of the sphere be r. Then,

   1. Volume = r³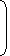 cubic units.
   2. Surface area = (4r²) sq. units.
6. HEMISPHERE

   Let the radius of a hemisphere be r. Then,

   1. Volume = r³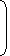 cubic units.
   2. Curved surface area = (2r²) sq. units.
   3. Total surface area = (3r²) sq. units.

      Note: 1 litre = 1000 cm³.

প্রতিটি লেকচারে নতুন নতুন লিখা যুক্ত হচ্ছে, তাই কাঙ্খিত কোন লিখা না পেলে দয়া করে কিছুদিন পর আবার ভিজিট করে দেখবেন।

লিখাতে কিংবা লেকচারে কোন ভুলত্রুটি থাকলে অথবা আপনার কাঙ্খিত লিখা খুঁজে না পেলেইশিখন.কম এর ফ্যানপেইজ অথবা নিচে কমেন্ট কর